Fibonacci Iterative vs. Recursive

Fibonacci series:

fib(n) = fib(n-1) + fib(n-2) → for n > 1
fib(n) = 1→ for n = 0, 1

Fibonacci can be solved iteratively as well as recursively

Recursive approach:

The recursive approach seems to be much simpler and smaller, but there is a caveat, as it is calculating the Fibonacci of a number multiple times.

Time Complexity:

The time complexity of the iterative code is linear, as the loop runs from 2 to n, i.e. it runs in O(n) time

Calculating the time complexity of the recursive approach is not so straightforward, so we are going to dive in

fib(n):
    if n <= 1
        return 1
    return fib(n - 1) + fib(n - 2)

for n > 1:
T(n) = T(n-1) + T(n-2) + 4 (1 comparison, 2 subtractions, 1 addition)

Let’s say c = 4 and try to first establish a lower bound by approximating that T(n-1) ~ T(n-2) , though T(n-1) ≥ T(n-2), hence lower bound

T(n) = T(n-1) + T(n-2) + c
     = 2T(n-2) + c    //from the approximation T(n-1) ~ T(n-2)
     = 2*(2T(n-4) + c) + c
     = 4T(n-4) + 3c
     = 8T(n-6) + 7c
     = 2^k * T(n - 2k) + (2^k - 1)*c
Let's find the value of k for which: n - 2k = 0
k = n/2
T(n) = 2^(n/2) * T(0) + (2^(n/2) - 1)*c
     = 2^(n/2) * (1 + c) - c
i.e. T(n) ~ 2^(n/2)

now for the upper bound, we can approximate T(n-2) ~ T(n-1) as T(n-2) ≤ T(n-1)

T(n) = T(n-1) + T(n-2) + c
     = 2T(n-1) + c    //from the approximation T(n-1) ~ T(n-2)
     = 2*(2T(n-2) + c) + c
     = 4T(n-2) + 3c
     = 8T(n-3) + 7c
     = 2^k * T(n - k) + (2^k - 1)*c
Let's find the value of k for which: n - k = 0
k = n
T(n) = 2^n * T(0) + (2^n - 1)*c
     = 2^n * (1 + c) - c
i.e. T(n) ~ 2^n

Hence the time taken by recursive Fibonacci is O(2^n) or exponential.

Space Complexity:

For the iterative approach, the amount of space required is the same for fib(6) and fib(100), i.e. as N changes the space/memory used remains the same. Hence it’s space complexity is O(1) or constant.

For Fibonacci recursive implementation or any recursive algorithm, the space required is proportional to the maximum depth of the recursion tree, because, that is the maximum number of elements that can be present in the implicit function call stack.

Below is a diagrammatic representation of the Fibonacci recursion tree for fib(6):

Recursion tree for Fibonacci of 6

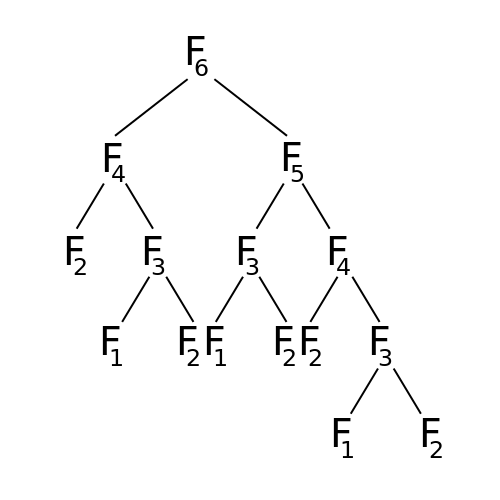
As you can see the maximum depth is proportional to the N, hence the space complexity of Fibonacci recursive is O(N).

If you like the post and want to learn more about Data Structures and Algorithms, Low-Level Design and High-Level Design to crack top product company interviews and get into FAANG, then I would highly recommend joining Scaler, where I am an Alumni and owe a lot of my success to them. Their curriculum is highly structured with teachers who are ex-Googlers, ex-Media.net etc. employees. You also get mentorship from the very best, working in your dream tech companies like FAANG. If you use the link my link to join Scaler, then you will get a course discount of Rs. 10,000 and I will get a cashback of the same amount. Do check out their course and take advantage of the classes provided by them to boost your career from the comfort of your home.

For more tips and algorithms check out my other content. Happy coding!!